互质：任意自然数a, b，若gcd(a, b) = 1，则a，b互质。

欧拉函数：1~N中与N互质的数的个数被称为欧拉函数，记为φ(N)。

若在算术基本定理中，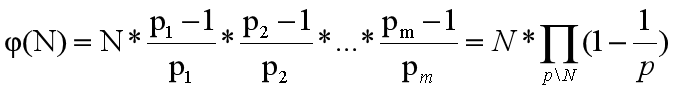

 

。

公式的证明用到的思想被称为容斥定理。在N的全部质因子上用容斥定理，即可得到1~N中不与N含有任何共同质因子的数的个数，也就是与N互质的数的个数。

 

根据计算式，只需要分解质因数，即可求出欧拉函数。

1 int phi(int x){ 2     int ans=x; 3     for(int i=2; i*i<=x; i++){ 4         if(x % i == 0){ 5             ans = ans * (i-1) / i; 6             while(x % i == 0) x /= i; 7         } 8     } 9     if(x > 1) ans = ans * (x-1) / x;10     return ans;11 }